David of Santa Barbara -- Violin Maker David Beard

 

Hi Again,

Time for a new post!

This discusses the older physical culture surrounding the great Old Cremona instrument making.  The focus is on the role of proportions in the works of Stradivari and the other making families.  It touches also on the divider tool, and on the old unit of length measure in Cremona, the oncia.

Cremona Revival Table of Contents Page //

Historical Making and Preliminary Topics
        1) --- Measurements & Proportions
        2) --- Instrument Shapes: Origins and Evolving Geometry
        3) --- Arts & Materia
        4) --- Making Traditions

 

--- Measurements & Proportions

The great Old Cremona making comes from a different time and context than our own, a different physical culture.  These differences of tradition and perspective run deep, carrying surprising consequences.

 Here, we’ll explore older notions of measurement and proportion.

 

 

 

 

 

 

 

 

 

 

 

To open a road to understanding the old making, we need to step away from our normal modern paradigm. We’ll explore how notions of measurement and proportion framed the older physical culture in ways that contradict assumptions of our own time.

**************************************

First off, we live in a modern world where reliable precision measurement and exact standard references of measure are generally readily available.  

Individually, we have easy access to good weight scales, pitch tuners, thermometers, accurate clocks, and precise length measurement. And, as a community, we go much further, measuring many things: the speed of sound, the speed of light, the wavelengths of light, the size of molecules and atoms, the distance of planets, etc.

But, in the time of Da Vinci, Andrea Amati, and Antonio Stradivari, these standardized resources of measurement didn’t exist. 

So, without our modern measurement standards and tools, how did those old Cremona masters accomplish such wonderful and finely detailed work?   To a great extent, they leaned less on fixed measurements, and more on proportional relationships.

To understand this, we must step away from our familiar context and explore their world, on their terms.  And, we’ll see how proportions were used more extensively. Fixed reference measurements were not yet internationally or even necessarily regionally standardized.  Necessarily, such measurements were central to the older physical culture than we are used to.

Now, we aren’t saying they didn’t have measure sticks. Measuring rods and measuring coils have existed from the most ancient times. But, they did not have our standardization of such reference units for measure.   Perhaps a king held the one reference measure for his realm.   Or the local guild held a reference for their craftsmen.  In some cases, various reference points might be coordinated. But, this was not a generally reliable thing.  

You couldn’t just say 10 feet and be sure the other fellow would understand that as exactly the same length you meant. Today terms like 440 hz, 50 Angstrom,  5 nanoseconds, 6.3 Mohs, 70 db, and 32 Fahrenheit all have globally standardized meaning now.  But in the time of the classical violin makers, these measurement resources didn’t yet exist.   The Amati, Guarneri, Ruggieri, and Stradivari families did their work in a very different world than ours.

 The circumstances for some types of measure were better than for others.  At least with measuring rods for length and with scale weights you have the possibility of directly comparing.   We can see and very easily determine if two reference sticks are basically the same length.   And, with weights, we can use a balance scale and compare if two reference weights match well or not.

Before modern times, other various types of measure were very rough, or indirect in method, or not possible at all. Temperature and time are two examples.  For time, various kinds of clocks existed, but were far from perfect.  You could have a sand glass to provide a reasonably repeatable unit of time for reference in your own work.  But, the measure of time was far from straight forward.   Temperature was even more difficult to manage.   Recipes might refer to cooking something ‘until it singes feather’, or ‘until the smoke goes from white to brown.’   Careful observation of the stages of boiling water can also give a reference point.  But there wasn't actually any method available to measure temperature.     

Interestingly, many of the foundations of our modern world’s measurement systems were developed during the same years as classical Cremona violin making, roughly 1550 to 1790.   But, the traditions of Northern Italian and general European instrument making culture originate before many of our modern measurement resources fully developed.  Things like clocks and thermometers and many other concepts and tools were still developing over this time.

Measurement of the frequencies of sounds developed even more slowly.   In Galileo’s day, corresponding to the early successes of Amati family violin making, the nature of sound as a series of pressure pulses was still not understood.   It wasn’t until the 1800s that we learned to measure the frequencies of sounds, after the entire two centuries or so of classical Cremona violin making development peaked and ended.

And this brings us to the primacy of ratio and proportion in earlier times.  In a world where the same unit of length could have an inconsistent meaning from town to town, or even from one guild to another within the same town, the relationships of proportions and ratios were universally consistent, reliable in  meaning.  ‘1/3’ was and is 1/3, everywhere, always.  But ‘1 foot’ wasn’t consistent.  The meanings of specific measures were generally inconsistent.

 ************************

This reliance on proportion above fixed measure has surprising consequences for design culture.

Today, even when we actually do design something using proportional ideas, we nevertheless tend to describe the design in absolute reference measures.   So, even if designing a book case using a 2 to 1 proportional idea, we tend to describe the design by say something like the book case is 6ft high by 3ft wide, instead describing the actual design idea by saying the case is twice as high as it is wide.  Similarly, with neck and body stops of an instrument we tend to say that the neck length of an instrument is 130mm, with the distance from the neck down to the bridge being 195mm.   But, in this way we bury the 2 by 3 proportional idea hiding in these numbers.  Such is our modern paradigm.   

The older physical culture tended more to reverse these priorities. A description of proportions expressed design more fundamentally than did a description of reference measures.  And, this difference has profound consequences.

***************************

In its way, pitch helps illustrate why early culture leaned more on ideas of ratio and proportion than we do today.

In musical culture, the primacy of proportions was doubly underscored.  For centuries, music developed with an understanding that musical intervals were deeply linked to numeric ratios.   But, the numeric measurement of pitch frequency wasn’t even possible yet.  We didn't even understand the physical nature of pitch nor pitch frequency yet.

Bach and Mozart were dead and gone before it was even possible to know the ‘frequency of a pitch’. They had note names like ‘a’, but not frequencies like A440 -- not even the concept of a pitch consisting of a measurable number of pulses of air pressure per second.   Yet, before the Caesars of Rome, people did understand that an octave interval is deeply associated with a ratio of 1 to 2, and that a perfect fifth is associated with a ratio of 2 to 3.   This link between musically meaningful intervals and ratios of numbers was understood since the days of Pythagoras in old Greece.

2,000 years before the actual measurement of pitch frequency was even possible, people figured out that objects that made sound, like strings or air pipes, would make good musical intervals if you varied the objects using simple ratios.

So, if you doubled, or halved the length of a pipe or a string, you got a higher or lower octave.   Or, when you tensioned a string with a weight, if you doubled the weight, again you got an octave interval.   And, people explored further.  

 They set up ‘monochords’ to play a single simple string, dividing the string's length in various ratios to learn the musical intervals that resulted.  In this way, they learned all the ratios associated with musical intervals.   They also found and explored harmonics of strings and pipes.  Which similarly are linked to simple integer ratios.

The old world of music navigated via ratios and proportions, not by fixed measure.  

 ******************************

Proportions and dividers were integral to the intellectual and artistic flowering of the Renaissance. We see them tied into the practical work of artists, architects, navigators, scientists, and military men.  And, we see these as symbols of social, intellectual, and philosophic leadership.  Old fashioned now, these were cutting edge concepts and tools.

These were the tools of Leonardo Da Vinci, Albrescht Durer, Luca Pacioli, Michelangelo, Leon Battista Alberti, Andrea Palladio, et al.  These same tools of ratio and dividers favored by the Renaissance appear abundantly in the works of ancients like Euclid, Pythagoras, Vitruvius, et al.  

Further, the importance of ratios, proportions, and dividers continued through past the time of tall sailing ships. For the Age of Enlightenment, these things acquired a further political significance, with the ‘compass and rule’ as symbols coming to represent a transition of power away from Church and Royals.  

This same transition brought on the end of the old system of guilds, apprentices, and masters, as well as the end of classical Cremona violin making.   But, socially these changes represented progress to the likes of Voltaire and the Encyclopedists.  Notably, the changes that ended classical Cremona making are the same changes that created the United States and the French Revolution. 

For the Founding Fathers, proportions and dividers were both essential tools for architecture, navigation, warfare, etc, as well as important symbols of the rising power and independence of individuals, separate from the ancient pillars of Church and Royal Nobles.

 ******************************************************

Following are some simple introductions to various ideas related to proportions and dividers. 

Dividers:

The idea of dividers is simply to walk off steps of equal length:

 

 

 

 

 

 

The reason we call them dividers is that this tool allows us to divide a given length into however many parts we choose. The second illustration here shows how to divide a length into five parts.  First, you guess at 1/5^th the length.  Then you test by walking this distance out.  You adjust your guess and retest as many times as needed until you successful ‘walk’ the original distance.

In short, ‘dividers’ create or ‘walk off’ equal parts.    

Ratios:

Ratios correspond to fractions.   They are comparisons of simple integers.  Physically, they represent comparisons of numbers of equal ‘parts’ of something like length, or anything else, for example weights.

            ‘4 to 1’  or   ‘4 by 1’  are the same as 4/1

            Similarly, ‘3 by 5’ is the same as  ‘3/5’

The first example compares 4 equal parts to 1 part.   The second compares 3 parts to 5 parts.

As noted, such ratios correspond to simple fractions of integers.  In consequence, all the complications and mathematics of fractions do actually apply.

Proportions:

Proportions are an expansion of the idea of comparing things, in order to enable comparing several items, using the same ‘equal parts’ as units.

In music for example, the interval between two notes is represented by a ratio.  But, when you combine several intervals to make a chord, then those are all represented by a proportion. A major third interval can for example be represented by the ratio 4 to 5. But, a simple triad might be represented by the proportion 4 to 5 to 6.

An alternative conception of ratio versus proportion is that a ratio tells us what part something is of a whole, what portion.   In this conception, a ratio is of like things, and compares an item to its whole. So, for example 1/20 of the whiskey keg might have been a sailor’s portion of the whiskey. That would be a ratio.  In contrast then, proportions compare things with a common unit, but not necessarily the same things, or just 2 of them.

Dot Notation:

One tradition notation for ratios and proportions distinguishes these by dots, using a single pair of dots for ratios (:), and doubled pairs for proportions (::).

i.e.  4:5 is the ratio behind a natural major third music interval.

       4::5::6 is a proportion giving a major triad chord.

Compass:

A compass is informally the same as a divider.  But, formally there are differences.   A compass marks out arcs or circles, so one leg is the pivot and one leg a marker of some sort.

Formally however, a divider has both legs as pivots to walk off equal parts. 

In practice a divider and a compass are reasonably interchangeable.  Particularly, you can drag one leg of a divider to mark out arcs, like a compass.

Compass and Rule Geometry:

‘Compass and rule’ is a reference to Euclid’s geometry.  As a theoretic geometry however, it differs some from the craftsman’s practical work.  Euclid’s theorems of geometry work for an abstract ideal of the ruler and compass.  In this abstract version, the ruler is infinite in length, and lacks any marks of distance.  And the compass can mark arcs from one point as center, and another point giving radius.  But, this theoretic compass does not retain the distance between these points.  As soon as you lift Euclid’s ideal compass from its center point, it forgets the width setting.  A real ‘divider’ of course retains this width, locks it in.

Sectors:

This tool combines ideas of dividers and proportions to make the Renaissance version of a calculator.   A sector has two arms like a divider.  But, these arms are marked with scale units.  Complex calculations of ratios can be made using a sector in combination with normal dividers.  Also, if the sector is marked out with special scales of length along its legs, other forms of special calculations can be made.

This was an important tool until roughly the time of WWI.  It’s also why various kinds of wooden rules were made with a hinged center pivot until modern times.  Such a hinged ruler can serve as a basic ‘sector’. 

 ********************************

Some Techniques:

 

 

*******************************************************

 Be sure, the various masters of the Renaissance exploited these resources to the fullest.

 

 Broadly, throughout the arts and sciences, the dividers and proportions were ever present tools of craft.

***************************

As we dig deeper into exploring proportions and divider methods in classical instrument making, some will think the practices too complicated or arcane.    

But, consider the larger cultural context. Dividers and proportions were the pinnacle tools for complex and serious work.    

The military general, the naval navigator, the surveyor and architect, all used these tools.  As did all the artisans from jeweler, to guilder, to master painters.

To illustrate the sophistication of usage in various fields, consider the case of music theory.  The usage of ratios in Renaissance and Baroque music studies became truly complex. 

The ratio complications of music theory stem from the ways simple intervals combine. Each exact interval corresponds to a ratio. Some of the combinations turn out as simple ratios themselves, but some don't. Also, the musical scale materials are cyclic. Sometimes we expect different combinations of intervals to end up on the same note, but sometimes the resulting ratios don't agree.  Renaissance musicians even studied the ratios that occur between slightly different versions of one note, called 'coma' ratios. 

In example, octave intervals combine or compound in simple clear ways, but other intervals do not.  That is, you can go up and down through many octaves of the same note, and aurally and theoretically, the lowest and highest octaves of the same note end up naturally agreeing with each.  

But, when you stack up (or compound) other intervals, difficulties develop.  When you chain up a series of perfect fifths, you will come to certain notes that in one sense aught to match other simple intervals, but they don’t.  The compounding gets complicated. 

Music theorists of this time explored the ratios behind all these things, thus learning way things don’t quite fit together. People like Zarlino and LanFranco wrote thoroughly about these musical details, laying bare the technical and harmonic advances behind the Ars Nova and the developments from a Medieval hexachordal scale system to full chromatic scales.  Some even explored microtonal systems.   Most accepted the conclusion that enharmonic difference are deeply embedded in our musical system, and that scales must be ‘tempered’ to strike balance between conflicting factors. 

*******************************

These were also the tools of the most expressive genius artists of the time.

We are used to thinking of the true artist as somehow above rules and order.   But once again, there is danger in letting modern assumptions apply to an older different world.

One can argue fairly well that throughout the time of the classical Cremona making, the geniuses of the arts operated not without or beyond the earthbound rules of their crafts, but rather in full mastery of the craft sides of their art.

Thus, in the Museo Galileo there is a drawing tool kit believed to have been Michelangelo’s.

And, when we dig through Leonardo Da Vinci’s notebooks, they are filled with practical observations of natural subjects, many expressed as size relationships in terms of simple ratios.

Indeed, in the icon ‘Vitruvian Man’ drawing we are seeing the great genius exploring simple size ratios between parts of a man.   And, in fact, he is exploring the ratios recommended by the Roman Architectural writer Vitruvius.   

The use of the dividers and of simple ratios and proportions has permeated the arts since ancient times.

In Leonardo’s characteristic reverse writing above the figure:

“Vetruvio, architect, puts in his work on architecture that the measurements of man are in nature distributed in this manner: that is a palm is four fingers, a foot is four palms, a cubit is six palms, four cubits make a man, a pace is four cubits, a man is 24 palms and these measurements are in his buildings. If you open your legs enough that your head is lowered by one-fourteenth of your height and raise your hands enough that your extended fingers touch the line of the top of your head, know that the centre of the extended limbs will be the navel, and the space between the legs will be an equilateral triangle.”

 And below:

 “The length of the outspread arms is equal to the height of a man; from the hairline to the bottom of the chin is one-tenth of the height of a man; from below the chin to the top of the head is one-eighth of the height of a man; from above the chest to the top of the head is one-sixth of the height of a man; from above the chest to the hairline is one-seventh of the height of a man. The maximum width of the shoulders is a quarter of the height of a man; from the breasts to the top of the head is a quarter of the height of a man; the distance from the elbow to the tip of the hand is a quarter of the height of a man; the distance from the elbow to the armpit is one-eighth of the height of a man; the length of the hand is one-tenth of the height of a man; the root of the penis is at half the height of a man; the foot is one-seventh of the height of a man; from below the foot to below the knee is a quarter of the height of a man; from below the knee to the root of the penis is a quarter of the height of a man; the distances from below the chin to the nose and the eyebrows and the hairline are equal to the ears and to one-third of the face.”

This approach of describing a complex design in terms of ratio relationships was not unique to Vitruvius, or his description of human proportions. It is reflective of one of the deepest differences between design principles from modern physical object culture and the older physical culture.    

Today, design tends to mean the specific exact size and shape of one instance of a kind of object. The design is one fully realized and fixed design, completed before any object is actually made. Then, in most cases, the design is used exactly to make a great many physical objects conforming entirely to this design.    

But in older physical culture, design tends to be more of an exemplar or even a recipe for making many variant designs of a type of object, but of any size or with different decoration or details as needed. And, the design ‘recipe’ does not necessarily need to be specifically realized before an object is made. 

Usually there was no intention to make many identical objects from a design.  It is mass production and factory style work environments that push us to prioritize highly regular and well squared parts.  Such parts facilitate the interchangeability of labor and components. But without the concerns of factory style production, there is no need for this.  Parts can all be different, and fitted uniquely in each case.  In the older culture of unique handmade production it is also possible to realize many specifics of a particular instance of the design recipe in the object itself, while it is being made.

This is one of the deepest differences between old and new making of physical objects. And, it is a difference embedded in the our modern preference for specific reference measure, versus the older preference to size by ratio relationship. A design in fixed measure, completely realized ‘a priori’ (ahead of time), favors modern mass production of many identical objects.    An exemplar design ‘recipe’, based on scalable ratio relationships, favors one off uniquely fitted creation of objects -- the old way of things.

A similar description in ratios of how to build a complex object can seen in Vitruvius’ ‘design recipe’ for building ballistae, large or small, plain or ornate.

And, one of the oldest technical descriptions for building an instrument is this exemplar drawing showing fundamentals for building a lute type instrument. Again, this is a pattern or ‘recipe’ that can be variously adapted.

Also, notice that the complicated curved shapes breakdown into the same sort of geometry of lines and circle arcs that fascinated the ancient Greeks.

 

 ****************

A curious thing about the culture of old Cremona violin making is that it exists only in the transition from a very old world into the beginnings of what becomes the modern world.  

Before roughly 1525, centuries old continuous cultural traditions were still developing to the point where the viola, cello, and violin could emerge.  When the violin family does appear, physical culture is still entirely connected to roots that reach all the way back to the ancient world.   But, at this moment the culture is also beginning to awaken and progress toward a very new world. The seeds of many new things are growing already.  And, some of this newness is part of the creation of the violin family.  The period of classical making exists only in this transition, after 1525 and before 1800. By roughly 1790, social and economic changes progressed enough to actually break the traditions and culture that enable the great classical making.  These traditions had previously been continuous for many centuries and generations, only slowly evolving.

You can see the differences between modern physical culture and the older physical culture by comparing almost any kind of object made in 1750 or earlier to the corresponding object made in 1825 or later.  It’s a seismic shift.

 

The older physical culture was different. 

Objects weren’t mass produced.  Each was uniquely handmade. 

Whether lowly and utilitarian or princely and fine, the labor and materials of an object were valued.  Artisans aimed to make objects that could give worthy and long service.  Particularly, work for the church or the court was often rich in materials.

From the artisans, artists, and craftsmen, we generally see objects with integrity, appropriateness, and even beauty.  But, this wasn’t an age of machine perfect production, nor of factory work.  In every feature of every object we see human hands. We see irregularities. We see abundant trace of the artisan in these objects.

There is a sharp contrast to later modern aesthetics of clean perfection, of well squared and true regularity, of equal exact symmetry.

***************************

Various masters of the past tried express design aesthetics with a few key principles.

Vitruvius for example identified ‘firmitas’, ‘utilitas’, and ‘venustas’ as principles for the architect.   We might understand these basically as ‘solidity/Integrity’, ‘usefulness’, and ‘pleasingness/beauty’.  Many Renaissance and later masters had similar lists, usually longer.   Such lists varied considerably.   

In example, around 1750 Hogarth listed six principles for ‘beauty’.  He gave his principles as 1) ‘fitness’, 2) ‘variety’, 3) ‘regularity’, 4) ‘simplicity’, 5) ‘intricacy’, and 6) ‘quantity’.   Many masters gave similar lists.   While these lists never seem to quite agree, still there are many shared themes running through. We see many echoes of Vitruvius, and many expressions of needs for both ‘unity’ and ‘variety’. 

While my personal biases are likely to sneak through, I will try to pull together some of the main themes seen:

Economy/Fitness/Appropriateness/Simplicity
---       As an aspect of unity, a clean simplicity of means can benefit design.

Harmony/Rhythm/Regularity/Integrity
---       Also an aspect of unity, relatedness between parts gives wholeness to variety

Emphasis/Movement/Variety/Intricacy
---       There is also some need to disrupt unity

Balance/Symmetry/Proportion
---       Further appeal to underlying order among elements, unity running through.

******************************

In this light, the significance of simple integer proportions seems natural, and of obvious appeal for the old masters.

Dividers and proportions were the tools for creating order and relationship among the parts of a work.  These gave the means to infuse work with 'rhythm', 'harmony', 'balance', 'symmetry', etc.

But let’s be cautious. Some of these old aesthetic values, like 'regularity' or 'symmetry', sound much like modern culture values of symmetry, regularity, squareness.  And, at least, they sound like very near neighbors to other modern values like 'precision', 'flawlessness', or 'perfection'.  

The older usage of such values differs some.  It is never about repeatability for mass production.  Words like 'harmony' and 'symmetry' are talking about a 'readable' relatedness among parts, about ratios and proportions embedded within design.  But, these older values do not extend to standardization and perfection of measure in the execution of work.  That is a modern value.

To understand this, let’s look again at Da Vinci’s Vitruvian man.   Under the main image we see a scale line drawn in.   This makes sense.   From the text, we know he is explicitly exploring the ratios from Vitruvius.  The scale makes sense in that context.

By sight, it appears the scale show the width of the images main square, that is the height of the man, divided into 4 parts.  The outer 4ths are then each divided into 6 parts.  And, on each side, the outer most 6^th is again divided in 4 parts.

All of this reads clearly enough. And, this drawn scale corresponds with the Vitruvian proportions.   The ‘cubit’ is a 4^th the man.  Our scale has 4ths.  A man is ’24 palms’.  Our 4ths are divided again by 6ths, giving 24ths or ‘palms’.   Fingers are described as 1/4^th a palm.  And again, the drawn scale shows this.

Everything reads beautifully and cleanly.    

But, to the modern measurer, it all fails.  

If we attach accurate scales to the drawing, then we plainly see how poorly Da Vinci has worked.  The main line of the scale is a bit bigger than the square, actually.  The 4ths of the line are irregular and not actually equal! Likewise, the finer subdivision are not truly exact or even.

This gets at a central difference between the older physical culture and our modern paradigm:   

The older work does not aim for perfect exact measurement, but it aims for and succeeds in ‘reading true’ to its own motivating proportional ideas.

In contrast, modern values tend to elevate perfection of actual measurement to its own sort of virtue.  Sometimes perhaps allowing such focus to be more important than other design motives.

Da Vinci shows us the opposite of modern values.  The essence of motivating proportional ideas is deeply honored.  But, exact precision by measure is only guesstimated.

We might sum up this contrast as ‘Accuracy to Proportion and Concept versus Precision by Measure and Reference’.

**************************

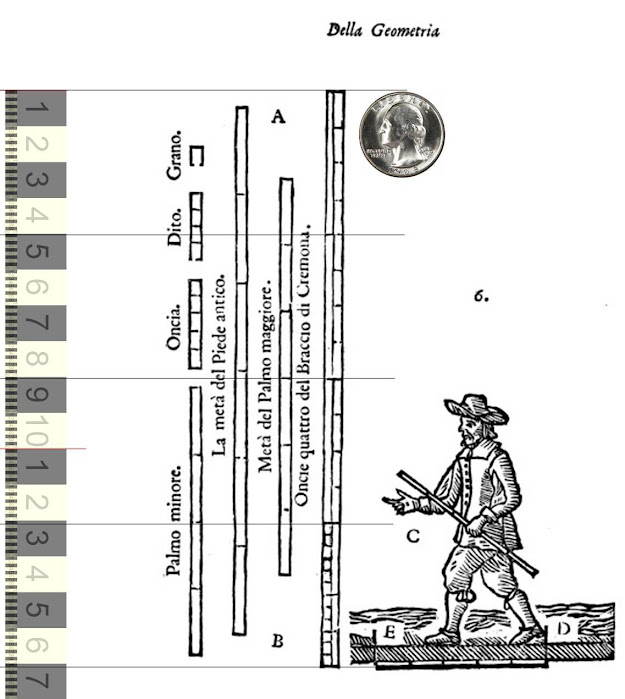
The Cremona Oncia: 

Various authors on violin making have suggested there was a Cremona ‘oncia’, somewhere close in size to 40mm in length.   

As we know, length units were not well standardized. (Discussion of Historical Oncia Units.  Wikipedia article on old Italian measure units.) 

In the Po river region, including Venice, Bresica, and Cremona, most of the units of measure derived from the units of old Rome.  For our purposes, we are most interested in the Braccio unit, divided into 12 oncia, which in turn each divide into 12 points. 

Our most direct evidence for a Cremona oncia comes with a curious connection to Antonio Stradivari himself.  Stradivari’s first wife, Francesca, was a young widow when she married Antonio.  Her first husband’s father was both an architect and mathematician, Alessandro Capra.  In 1717, Capra published a book of architecture which includes an illustration of the Cremona measurement system, including a life size print of the ped and oncia.

This illustrates a ped with an oncia of approximately 40.25mm.   But of course, the potential margin of error is considerable.   There also had been a town square pedestal with the same ped and oncia carved into it as a community reference.   By report, this pedestal basically agreed with Capra’s book.

After using error reduction analysis, and looking across a fairly large number of telling example instruments and artifacts, I would suggest that the actual oncia in Stradivari’s shop was likely in the range of 40.05mm +/- .1mm.  Further, it’s unlikely that rulers from one shop to another were truly consistent. Even rulers within one shop likely varied.

Still, it appears that most features in a classical violin design were sized and placed by proportional relationships rather than by specific fixed measurements. 

One of the few exceptions seems to be the basic framing of instrument sizes.  When analyzed, body lengths generally, and widths occasionally, seem to be keyed off initial oncia measures.  Perhaps this was considered part of the design concept, a choice that helped determine the type and nature of an instrument.   

Thus, we see classical violas mostly tied to a key length between 10 and 12 oncia.  And we see piccolos and special small violins in a range keyed from over 7 to under 8 + ½ oncia.  But, proper violins were keyed between 9 and 9 – ½ oncia.  These key lengths are generally chosen as some number of oncia units, adjusted by a logic ‘portion’ of an oncia.  So, with violins, the key lengths are 9, reduced by a one part of an oncia like 1/6, ¼, 1/3, ½, etc. 

We also see oncia based measures in the various insets associated with the designs.  So the inset of the mould compared to the outer edge of the instruments, and the insets of the purfling inlays tend to be base on 1/12 oncia units called ‘points’.  Measures like 1 or 2 points, as well as measures like 1 ½ point, or 1 1/8 point, etc. are all common in classical instrument insets.

These insets and body lengths are initial choices that help frame the basic size of an instrument.  However, all the further design features and details of these classical instruments were worked using traditional recipes of proportions and geometry.

*****************

Hopefully we’ve opened a window onto some of the design principles of the older physical culture.

Very humanly satisfying results can be achieved by fitting parts uniquely one to another, rather than by making all square and regular.

Placing proportional relationships above specific fixed measurements can help bring balance and harmony to designs.  Readable differences between ratios, like 3:4 versus 4:5 can bring beauty and structure to the finest details of any design.

Design does not have to be approached in the modern way, as fully realized plans worked out beforehand to a specific size and predetermining all details.

Design can instead be seen as scalable recipes of proportions and relationships that allow you to build many examples, with differing sizes, decorations, and details.  Much can be chosen interactively during the building process.